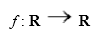Funções reais de variáveis reais
Introdução
Uma função é uma aplicação entre conjuntos, As funções descrevem fenómenos numéricos e podem representar-se através de gráficos sobre eixos cartesianos. O gráfico de uma função permite ver, muito facilmente, toda a sua evolução.
O presente tópico irá debruçar mais sobre funções reais de variável real, onde veremos que uma função real de variável real é uma função em que tanto os elementos do conjunto de partida ou conjunto dos objectos como os do conjunto de chegada ou conjunto imagem são números reais, isto é, pertencem ao conjunto R.
Funções reais de variáveis reais
Função
Uma função é uma aplicação entre conjuntos. As funções descrevem fenómenos numéricos e podem representar-se através de gráficos sobre eixos cartesianos. O gráfico de uma função permite ver, muito facilmente, toda a sua evolução. Porém, por vezes, pode ser mais cómodo trabalhar com a equação ou fórmula da função, já que com ela temos à nossa disposição o conjunto de operações que devemos aplicar à variável independente, normalmente representada por x, para obter a variável dependente, normalmente representada por y. Podemos imaginar que uma função é uma máquina em que introduzimos um número x do conjunto de partida, dela saindo o número f(x).
Funções Reais de Variável Real
Uma função real de variável real é uma função em que tanto os elementos do conjunto de partida ou conjunto dos objectos como os do conjunto de chegada ou conjunto imagem são números reais, isto é, pertencem ao conjunto R, e representa-se por:
As funções f(x) = x + 3, f(x) = x2 + 2x + 1, f(x) = 3x + 1/2, são exemplos de funções reais de variável real. Se dermos a x um valor real, ao realizar as operações obteremos sempre um número real f(x).
Pode acontecer que nem todos os números reais tenham imagem pela função. O conjunto formado pelos números reais que têm imagem chama-se domínio. Em geral, uma função real de variável real tem a seguinte expressão:
sendo A um subconjunto de R, que irá corresponder ao domínio da função.
Representação Gráfica de uma Função
Dado que o conjunto dos números reais se pode representar sobre uma recta, o método de coordenadas cartesianas serve para representar funções.
Observemos os gráficos das figuras. Como podemos observar, a variável independente x é representada sobre o eixo das abcissas e a variável dependente y sobre o eixo das ordenadas.
Função do 1º grau
Definição
Chama-se função polinomial do 1º grau, ou função afim, a qualquer função f de IR em IR dada por uma lei da forma f(x) = ax + b, onde a e b são números reais dados e a 0.
Na função f(x) = ax + b, o número a é chamado de coeficiente de x e o número b é chamado termo constante.
Veja alguns exemplos de funções polinomiais do 1º grau:
f(x) = 5x - 3, onde a = 5 e b = - 3
f(x) = -2x - 7, onde a = -2 e b = - 7
f(x) = 11x, onde a = 11 e b = 0
Gráfico
O gráfico de uma função polinomial do 1º grau, y = ax + b, com a 0, é uma reta oblíqua aos eixos Ox e Oy. Por exemplo, vamos construir o gráfico da função y = 3x - 1:
Já vimos que o gráfico da função afim y = ax + b é uma recta.
O coeficiente de x, a, é chamado coeficiente angular da reta e, como veremos adiante, está ligado à inclinação da recta em relação ao eixo Ox.
O termo constante, b, é chamado coeficiente linear da recta. Para x = 0, temos y = a • 0 + b = b. Assim, o coeficiente linear é a ordenada do ponto em que a recta corta o eixo Oy.
Rectas perpendiculares
Duas rectas t: x – y + 3 = 0 e u: x + y – 3 = 0 serão perpendiculares se possuírem um ponto comum e nesse encontro for formado um ângulo de 90°, veja o gráfico que demonstra essa perpendicularidade.
Se representarmos duas rectas perpendiculares em um plano cartesiano e levarmos em consideração os seus coeficientes angulares, perceberemos que não é preciso representar duas rectas no plano cartesiano para verificar se são perpendiculares ou não, basta comparar os seus coeficientes angulares.
As rectas t e u, representadas no plano cartesiano acima, possuem os respectivos coeficientes angulares mt = 1 e mu = -1, considerando que a recta t foi formada pela união dos pontos (3,0) e (0,-3) e a recta u formada pelos pontos (3,0) e (0,3).
Comparando os dois coeficientes angulares iremos perceber que mt é o oposto inverso de mu.
mt = 1 e mu = -1.
Considere as rectas perpendiculares r e s com os seguintes coeficientes angulares mr = 2 e ms = -1/2, elas serão consideradas perpendiculares, pois os valores de seus coeficientes é o oposto do inverso do outro.
Veja a demonstração da relação feita entre os coeficientes angulares de duas rectas perpendiculares.
Considere duas rectas perpendiculares v e p, veja a representação gráfica dessas duas rectas:
O ângulo de inclinação da recta v será igual a β e o da recta p será 90° + β, pois é o ângulo externo ao triângulo formado pelo ponto de intersecção das duas rectas com o eixo Ox. Com essas informações podemos dizer que o coeficiente angular da recta v será mv = tg β e o coeficiente da recta p será mp = tg (90° + β), aplicando as fórmulas de adição de arcos teremos:
Portanto, o coeficiente angular da reta p será: mp = -1 / tg β. Dessa forma podemos escrever que:
mv = tg β e mp = -1 / tg β, ou seja, duas retas serão perpendiculares se, somente se, seus coeficientes angulares forem iguais ao oposto do inverso do outro coeficiente.
Rectas Paralelas
No estudo analítico da reta não podemos deixar de falar das posições relativas entre retas. Dadas duas ou mais retas do plano, elas podem ser paralelas, concorrentes, coincidentes ou concorrentes perpendiculares. Abordaremos aqui o paralelismo de retas, assunto que sempre intrigou matemáticos de todas as épocas. Sabemos que duas retas são paralelas quando são equidistantes durante toda sua extensão, não possuindo nenhum ponto em comum.
Dessa forma, considere duas retas, r e s, no plano cartesiano.
As retas r e s são paralelas se, e somente se, possuírem a mesma inclinação ou seus coeficientes angulares forem iguais.
Utilizando a linguagem matemática:
Uma maneira mais simples de verificar se duas retas são paralelas é comparar seus coeficientes angulares: se forem iguais as retas são paralelas.
Exemplo 1. Verifique se as retas r: 2x + 3y – 7 = 0 e s: – 10x – 15y + 45 = 0 são paralelas.
Solução: Vamos determinar o coeficiente angular de cada uma das retas.
Reta r: 2x + 3y – 7 = 0
Para encontrar o coeficiente angular precisamos isolar y na equação geral da reta.
Funções do 2º Grau
Definição
Chama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR em IR dada por uma lei da forma f(x) = ax2 + bx + c, onde a, b e c são números reais e a 0. Vejamos alguns exemplos de funções quadráticas:
- f(x) = 3x2 - 4x + 1, onde a = 3, b = - 4 e c = 1
- f(x) = x2 -1, onde a = 1, b = 0 e c = -1
- f(x) = 2x2 + 3x + 5, onde a = 2, b = 3 e c = 5
- f(x) = - x2 + 8x, onde a = -1, b = 8 e c = 0
- f(x) = -4x2, onde a = - 4, b = 0 e c = 0
Gráfico
O gráfico de uma função polinomial do 2º grau, y = ax2 + bx + c, com a 0, é uma curva chamada parábola.
Por exemplo, vamos construir o gráfico da função y = x2 + x:
Primeiro atribuímos a x alguns valores, depois calculamos o valor correspondente de y e, em seguida, ligamos os pontos assim obtidos.
x
|
y
|
-3
|
6
|
-2
|
2
|
-1
|
0
|
-1/2
|
-1/4
|
0
|
0
|
1
|
2
|
2
|
6
|
Observação:
Ao construir o
gráfico de uma função quadrática y = ax2 + bx + c, notaremos
sempre que:
- se a > 0, a parábola tem a concavidade voltada para cima;
- se a < 0, a parábola tem a concavidade voltada para baixo;
Bibliografia
- 1.LIMA, Elon Lages. Curso de Análise, vol. 1. Instituto de Matemática Pura e Aplicada.Rio de Janeiro: Projeto Euclides, 1976.
- 2.LIMA, Elon Lages et al. A Matemática do Ensino Médio, vol. 1. Coleção do Professor de Matemática. Rio de Janeiro: SBM, 1996.