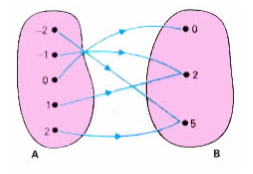
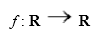Dada uma função f: A B, dizemos que f é par se, e somente se, f(x)=f(-x) para todo x A. Ou seja: os valores simétricos devem possuir a mesma imagem. O diagrama a seguir mostra um exemplo de função par:
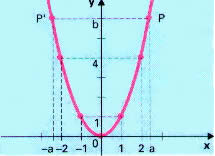
Por exemplo, a função f: IR IR definida por f(x)=x2 é uma função par, pois f(x)=x2=(-x)2=f(-x). Podemos notar a paridade dessa função observando o seu gráfico:
Notamos no gráfico que existe uma simetria em relação ao eixo vertical. Elementos simétricos têm a mesma imagem. Os elementos 2 e –2, por exemplo, são simétricos e possuem a imagem.
Por outro lado, dada uma função f: A B, dizemos que f é ímpar se, e somente se, f(-x)=-f(x) para todo x A. Ou seja: valores simétricos possuem imagens simétricas. O diagrama a seguir mostra um exemplo de função ímpar:
Função homográfica
As seguintes funções tem algum em comum:
Operações com funções
Também é possível realizar operações com funções:
Operações de soma, diferença, produto, quociente, e até competências.
- Soma de funções : aqui adicionam-se imagens de um mesmo objecto por funções diferentes. Exemplo : ( f + g ) (2) = f(2) + g(2) = ... + ...
- Diferença de funções : aqui subtraem-se imagens de um mesmo objecto por funções diferentes. Exemplo : ( g - h ) (-1) = g(-1) - h(-1) = ... - ...
- Produto de funções : aqui multiplicam -se imagens de um mesmo objeto por funções diferentes. Exemplo : ( f x h ) (5) = f(5) x h(5) = ... x ...
- Quociente de funções : aqui dividem-se imagens de um mesmo objecto por funções diferentes. Exemplo : ( j : i ) (0) = j(0) : i(0) = ... : ...
- Potência de uma função : a imagem de um objecto também pode ter potência pela mesma função! Exemplo : f "elevado ao quadrado" (-4) = [ f(-4)] "elevado ao quadrado" = ... "elevado ao quadrado"
Transformações lineares
Em Matemática, uma transformação linear é um tipo particular de função entre dois espaços vectoriais que preserva as operações de adição vectorial e multiplicação por escalar. Uma transformação linear também pode ser chamada de aplicação linear ou mapa linear. No caso em que o domínio e contradomínio coincidem, é usada a expressão operador linear. Na linguagem da álgebra abstracta, uma transformação linear é um homomorfismo de espaços vectoriais.
Função linear
Função linear é a função matemática que possui duas propriedades:
Adictividade:
f (x+x^i) = f (x)+f(x^i)
Homogeneidade:
f (ax)=af (x).
Em suma: f (ax+〖bx〗^i )=a*f (x)b*f (x^i).
As funções lineares são funções cujo gráfico é uma recta que atravessa a origem do plano cartesiano, isto é, em que b=0.
Definição
Chama-se função linear à função definida por uma equação da forma y=ax em que a é um número real.
y é a variável dependente e a variável independente;
a é o coeficiente angular
Nota: geralmente os economistas chamam a qualquer reta da forma y=mx+b uma função linear. No entanto, o conceito puro matemático, requer que a ordenada na origem seja zero para que a função seja considerada linear. Quando b é diferente de zero, passa-se a chamar de função afim.
A definição mais geral de função linear é feita no contexto da álgebra linear, e depende do conceito de espaço vetorial.
Função Exponencial e Logarítmica
Seja $latex a\in{\mathbb R}^+\setminus\{1\}. Chamamos função exponencial de base à função real de variável real.
O seu domínio é e o contradomínio é . A função é injetiva e sua monotonia depende do valor de . Em particular, se a função é estritamente crescente, enquanto que se a função é estritamente decrescente.
Exemplo: Representações dos gráficos de algumas funções exponenciais com base maior que 1:
Em particular, quando , chamamos logaritmo Neperiano ao logaritmo de base e representa-se usualmente por . Temos se e só se . No caso de a base ser 10 representa-se simplesmente por .
É necessário, no entanto, ter algum cuidado com a notação, pois alguma bibliografia opta por para representar o logaritmo Neperiano.
Funções Trigonométricas
Função Seno
Dado um ângulo cuja medida é dada em radianos é x, chamamos de função seno a função que associa a cada x ∈ R o número (senx) ∈ R. Indicamos essa função por:
f(x) = sen(x)
O gráfico da função seno, no plano cartesiano, será uma curva denominada senóide. Atribuindo valores ao arco x, pode-se chegar ao gráfico.
Propriedades:
- Domínio: R
- Imagem: [-1;1]
- Período: 2πrad
Função Co-seno
Dado um ângulo cuja medida é dada em radianos é x, chamamos de função co-seno à função que associa a cada x ∈ R o número (cosx) ∈ R. Indicamos essa função por:
f(x) = cos(x)
O gráfico da funcão co-seno, no cartesiano, será uma curva denominada co- senóide. Atribuindo valores ao arco x, pode-se chegar ao gráfico.
Propriedades:
- Domínio: x≠kπ+π2
- Imagem: R
- Período: π rad
Derivadas das funções trigonométricas inversas
Um problema comum em trigonometria é achar um ângulo cujas funções trigonométricas são conhecidas.
Problemas deste tipo envolvem a computação de funções arco, tais como arcsen x, arccos x, arctg x, e assim por diante. Consideremos esta ideia do ponto de vista de funções inversas, com a meta de desenvolver fórmulas de derivadas para as funções trigonométricas inversas.
Identidades para funções trigonométricas inversas
Se interpretamos x como um ângulo medido em radianos cujo seno é x, e se aquele ângulo for não negativo, então podemos representar x como um ângulo em um triângulo retângulo, no qual a hipotenusa tem comprimento 1 e o lado oposto ao ângulo de tem comprimento x (figura a). Pelo Teorema de Pitágoras, o lado adjacente para o ângulo tem comprimento .
Além disso, o ângulo oposto a é , uma vez que o co-seno daquele ângulo é x (figura b). Este triângulo motiva várias identidades úteis, envolvendo funções trigonométricas que são válidas para . Por exemplo:
Analogamente, x e x podem ser representadas com ângulos de triângulos retângulos mostrados na figura c e d. Esses triângulos revelam mais identidades úteis, como por exemplo:
Composição de Funções
Sabemos que uma função é uma relação existente entre duas variáveis, onde uma depende do valor da outra, formando assim pares ordenados que podem ser representados no plano cartesiano. Observe alguns exemplos de funções e suas definições:
- f(x) = 2x + 1 → note que f leva cada valor de x ao resultado 2x + 1.
- g(x) = 2x → note que f leva cada valor de x ao resultado 2x.
Mas, e se quisermos chegar a um determinado resultado aplicando um número real sucessivamente à lei das funções: f e g? Para esse tipo de situação utilizamos as propriedades de uma função composta, nesse caso devemos originar uma nova função, observe: h(x) = g(f(x)), função h é a composta de g com f.
Matematicamente falando, temos que f: A → B e g: B → C, denomina a formação da função composta de g com f, h: A → C. Dizemos função g composta com a função f, representada por gof.
- f(x) = 2x + 1 e g(x) = 2x
- h(x) = g(f(x))
- h(x) = g(2x+1)
- h(x) = 2 * (2x+1)
- h(x) = 4x + 2
Exemplo 1
Dada as funções f e g de domínio real definidas por f(x) = 3x – 2 e g(x) = – 4x + 1. Determine a lei que define:
- f(g(x)) → f(– 4x + 1) → 3(– 4x + 1) – 2 → –12x + 3 – 2 → –12x +1
- g(f(x)) → g(3x – 2) → –4(3x – 2) + 1 → –12x + 8 + 1 → –12x + 9
Exemplo 2
Sejam as funções f(x) = 2x – 6 e g(x) = x + 10, determine o valor de:
- f(g(2) )→ f(2 + 10) → f(12) → 2*12 – 6 → 24 – 6 → 18
- f(g(5) → f(5 + 10) →f(15) → 2*15 – 6 → 30 – 6 → 24
- g(f(–6)) → g(2*(–6) – 6) → g(–12 – 6) → g(–18) → –18 + 10 → –8
- g(g(3) → g(3 + 10) → g(13) → 13 + 10 → 23
Conclusão
Findo trabalho pude concluir que uma função é uma relação especial, que é definida da seguinte maneira: sejam dois conjuntos A e B, tais que para todo elemento x pertencente a A, haja uma correspondência de um elemento y pertencente a B. Essa correspondência é a função.
No seio do mesmo pude perceber que podemos designar função como uma relação entre dois conjuntos, representada por uma lei de formação, que associa os valores de x e y. De acordo com a lei de formação, cada valor de y depende do valor de x, essa relação de dependência é a principal característica de uma função. O estudo das funções exige conhecimentos básicos, que ajudam na interpretação de situações problemas e desenvolvimento de cálculos.
Bibliografia
- LIMA, Elon Lages. Curso de Análise, vol. 1. Instituto de Matemática Pura e Aplicada.Rio de Janeiro: Projeto Euclides, 1976.
- LIMA, Elon Lages et al. A Matemática do Ensino Médio, vol. 1. Coleção do Professor de Matemática. Rio de Janeiro: SBM, 1996.
- www.semnegativa.blogspot.com