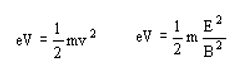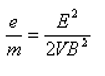Força de Lorentz
Introdução
No electromagnetismo, há uma lei que permite calcular o campo magnético a partir de uma distribuição de densidade de corrente elétrica ou de uma corrente elétrica, essa lei denomina-se Lei de Ampére.
A Força de Lorentz é a superposição da força elétrica, proveniente de um campo elétrico, com a força magnética, devida a um campo magnético, que atuam sobre uma partícula carregada eletricamente se movendo no espaço.
Portanto este trabalho visa abordar um tema que diz respeito à Força de Lorentz e Ampére.
Força de Lorentz
Geralmente os textos introdutórios sobre magnetismo iniciam com um histórico da descoberta do fenômeno, ocorrida na cidade de Magnésia, por volta do ano 121 D.C. Tanto o Halliday-Resnick quanto o Sears-Zemanski fazem esse tipo de abordagem.
Do ponto de vista formal, devemos ter em mente que é impossível tratar cargas elétricas em movimento sem levar em consideração a existência do campo magnético. Veremos logo adiante que cargas em movimento criam um campo magnético. Por outro lado, havendo um campo magnético em determinada região do espaço, este exercerá uma força sobre uma carga em movimento.
Existem duas formas básicas de criação de um campo magnético. A primeira tem a ver com a descoberta do fenômeno; trata-se do campo de um ímã permanente. A segunda forma tem a ver com o campo criado por uma carga em movimento; trata-se do campo criado por uma corrente elétrica.
Não importa, para o momento, qual a fonte de criação, o que importa é que dado um campo magnético, B, este exerce uma força sobre uma carga, q, em movimento, dada por F = qvxB onde v é a velocidade da carga. A força magnética é nula em duas circunstâncias:
- Carga estacionária (v=0);
- Velocidade paralela ao vetor campo magnético.
No caso geral, em que temos um campo elétrico, E, e um campo magnético, a força sobre uma carga em movimento é dada por:
É conhecida como força de Lorentz.
A DESCOBERTA DO ELÉTRON
A expressão foi usada por Thomson quando este realizava os trabalhos que resultaram na descoberta do elétron. Thomson usou um campo elétrico perpendicular a um campo magnético, para desviar o feixe de elétronsnumtubo de raios catódicos.
Joseph John Thomson (1856-1940), descobriu o elétron em 1897. Ganhou o Prêmio Nobel de física de 1906.
Pela eq. (8.2) vê-se que a força elétrica é perpendicular à força magnética. Controlando-se os parâmetros externos, E, B e v, é possível fazer
FE=FB eE=evB v=E/B.
A velocidade dos elétrons resulta da aceleração através de um potencial V, tal que:
Das expressões acima, obtém-se:
A razão entre a carga e a massa do elétron, ou de qualquer partícula carregada que penetre no tubo de raios catódicos, é calculada através de parâmetros controlados experimentalmente. Estes são ajustados de tal forma que o feixe permaneça em linha reta, isto é, de tal forma que a força elétrica equilibre a força magnética.
O EFEITO HALL
A expressão também permitiu a descoberta do efeito Hall que, como veremos, é extremamente útil na indústria microeletrônica.
A figura esquematiza o arranjo experimental para o estudo do efeito Hall. Tem-se uma fita condutora com seção reta A (=Ld) através da qual circula um feixe de elétrons com velocidade v.
Aplicando-se um campo magnético na direção horizontal, conforme indicado na figura, resulta numa força magnética na direção perpendicular ao movimento eletrônico, no sentido de cima para baixo. Esta força fará com que o movimento dos elétrons seja desviado para baixo. Com o tempo, cargas negativas acumulam-se na face inferior, e cargas positivas na face superior.
O excesso de cargas positivas e negativas, funciona como um capacitor de placas paralelas, com um campo elétrico conhecido como campo Hall. Chegará um momento em que a força Hall equilibra a força magnética,
qEH = qvB
Usando a eq. (6.3), J=nqv, e a definição da densidade de corrente, J=i/A, obtém-se
O efeito Hall permite a obtenção de dois resultados importantes. Em primeiro lugar, é possível determinar o sinal da carga dos portadores, bastando medir a diferença de potencial entre as superfícies superior e inferior. Em segundo lugar, a eq. (8.4) fornece o valor da densidade de portadores.
Esses dois resultados são de extrema importância na indústria eletrônica, pois permite a fabricação de dispositivos que dependem do tipo (elétrons ou lacunas) e da quantidade de portadores.
MOVIMENTO DE UMA CARGA NUM CAMPO MAGNÉTICO
A equção mostra que se a velocidade da partícula tiver a mesma direção do campo magnético, a força será nula, resultando nummovimento retilíneo uniforme. Por outro lado, se o ângulo entre o vetor velocidade e o vetor campo magnético for diferente de zero, podemos decompor o vetor velocidade em duas direções: uma na direção de B, e outra perpendicular. Isto é, A9
Portanto, o movimento de uma partícula, de massa m e carga q, numa região do espaço onde existe um campo magnético, é sempre composto de um movimento retilíneo uniforme e de um movimento circular. Este tipo de movimento é esquematizado na figura 8.3. Como se vê a força centrípeta, que proporciona o movimento circular, é igual à força magnética.
Assim, a partícula movimenta-se num círculo com raio
r = mv/qB (8.5a)
Da relação v=wr, obtém-se a velocidade angular
w = qB/m (8.5b)
Da relação w=2pf, obtém-se a freqüência
F = qB/2pm (8.5c)
e o período
T = 1/f = 2pm/qB (8.5d)
FORÇA DO AMPERE
No eletromagnetismo clássico, a lei de Ampére permite calcular o campo magnético a partir de uma distribuição de densidade de corrente elétrica , ou de uma corrente elétrica , ambas estacionárias (independentes do tempo). A partir da Lei de Biot-Savart é possível calcular o campo magnético associado a uma distribuição estacionária de corrente somando-se as contribuições ao campo de todos os elementos infinitesimais de corrente ao longo do circuito em questão. No caso de uma distribuição complicada de correntes o cálculo pode ser bastante trabalhoso e, em muitos casos, exigir o uso de um computador. Entretanto, se a distribuição possui algum tipo de simetria podemos usar a Lei de Ampére para determinar o campo magnético total, o que facilita consideravelmente os cálculos. O nome da lei é um reconhecimento ao físico francês André-Marie Ampére que a descobriu em 1826.
Motivação histórica
Experimento de Oersted
Em 1819, o físico Dinamarquês Hans Christian Oersted, estudando a ação de uma corrente elétrica sobre um imã, colocou uma bússola (agulha imantada) perpendicular ao fio retilíneo por onde passava corrente, não observando qualquer efeito. Todavia, descobriu que quando colocada paralelamente ao fio a bússola sofria uma deflexão, acabando por orientar-se perpendicularmente a ela. Por conseguinte, uma corrente produz um campo magnético. Os resultados de Oersted foram usados pelo jovem físico André Marie Ampère para formular a Lei de Ampère2 . No caso de um fio retilíneo muito longo transportando corrente, as linhas de campo magnético são círculos em planos perpendiculares ao fio, e a a orientação de tais linhas pode ser obtida por meio da regra da mão direita.
Determinação do campo magnético B
Analogamente ao caso de um sistema elétrico com elevado grau de liberdade em que a utilização da Lei de Gauss simplifica enormemente a determinação do campo elétrico, a lei de Ampère pode ser usada para determinar B, numsistema de correntes estacionárias com alguma simetria. Uma vez que A11, as linhas de força magnéticas são necessariamente fechadas (não existem monopólos magnéticos). Um exemplo são as linhas de forças circulares ao redor do fio retilíneo por onde passa uma corrente elétrica. O resultado da experiência de Ampère diz que a circulação de ao longo de uma curva C é proporcional à intensidade de corrente I que atravessa a curva (também denominada circuito amperiano). É importante destacar que isso só vale para correntes estacionárias. A lei de Ampère na forma integral pode ser escrita como:
permitindo sua determinação via Lei de Ampère. Nas circunstâncias em que ela funciona, é de longe o método mais rápido; caso contrário, deve-se recorrer à Lei de Biot-Savart 3 . As configurações de corrente nas quais a Lei de Ampère pode ser aplicada são:
- Linhas retas infinitas;
- Planos infinitos;
- Solenoides infinitos;
- Toroides.
Campo gerado por um cilindro condutor de raio R
Temos uma distribuição de corrente com simetria cilíndrica. No caso de um condutor longo, retilíneo e delgado que transporta corrente elétrica I as linhas de campo magnético devem ser círculos concêntricos com o eixo do condutor. O módulo de B em todos os pontos do percurso de integração é tangencial à circunferência, portanto a integral de linha terá valor A18, onde é o raio de uma circunferência imaginária. Considere A19 de forma que densidade de corrente é:
Campo de um solenoide infinito
Um solenoide é constituído por um enrolamento helicoidal de fio sobre um núcleo, geralmente com uma seção reta circular. É possível ter centenas ou milhares de espiras enroladas de forma compacta, de modo que cada espira se comporta como uma espira circular. As linhas de campo próximas do centro do solenoide são aproximadamente paralelas, indicando um campo magnético quase constante. Já na região externa ao solenoide, as linhas de campo são mais espaçadas, gerando um campo magnético mais fraco. O solenoide conduz uma corrente e possui espiras por unidade de comprimento. No caso de um solenóide infinito ou muito longo, o campo pode ser tomado como nulo fora do solenóide e uniforme na região interior.
Usando a Lei de Ampère temos:
Campo de um solenoide toroidal
Ilustração de um toróide de seção retangular
Um solenoide toroidal ou toroide é um solenoide que conduz uma corrente através de um enrolamento com espiras em torno de um núcleo em forma de rosca. Com uma aproximação idealizada, a simetria circular da configuração nos leva a concluir que as linhas de campo magnético são circunferências concêntricas com o eixo do toroide. Esta argumentação é válida porque consideramos o fluxo da corrente através da periferia do toroide desprezível. O campo magnético de um toroide está inteiramente confinado ao espaço no interior das espiras (o campo é zero fora do toroide).
Considere que o campo magnético seja tangente à circunferência e que a integral
Conclusão
Após a compilação de colectânea das informações, concluiu-se que o primeiro relato em que se encontra a fórmula do que hoje chamamos de força de Lorentz data de 1864, quando o físico escocês James Clerk Maxwell apresentou um importante trabalho à Roya lSociety intitulado A Dynamical Theory of the Eletromagnetic Field.
Constatou-se também que essas duas forças, influenciam muito nos cálculos do campo magnético. Do ponto de vista formal, devemos ter em mente que é impossível tratar cargas elétricas em movimento sem levar em consideração a existência do campo magnético.
No caso de uma distribuição complicada de correntes o cálculo pode ser bastante trabalhoso e, em muitos casos, exigir o uso de um computador. Entretanto, se a distribuição possui algum tipo de simetria podemos usar a Lei de Ampére para determinar o campo magnético total, o que facilita consideravelmente os cálculos.
Bibliografia
- Halliday, D. e Resnick, R. Fundamentos de Física,v.2,8a ed. GEN|LTC
- Tese de José Edmar - USP, "Sobre a Força de Lorentz, Os Conceitos de Campo e a "Essência" do Eletromagnetismo Clássico.
- H. MoysésNussenzveig, Curso de Física Básica, vol 3, Editora EdgardBlücher, LTDA (1999)
- http://www.escolademoz.com
Encomende já o seu trabalho!!!
+258 84 67 22 756